Opened 8 years ago
Last modified 6 years ago
#16658 new enhancement
Add highway=corridor, attraction=animal, man_made=water_tap
| Reported by: | Don-vip | Owned by: | team |
|---|---|---|---|
| Priority: | normal | Milestone: | |
| Component: | Internal preset | Version: | |
| Keywords: | highway corridor attraction animal tourism historic citywalls | Cc: | Klumbumbus |
Description (last modified by )
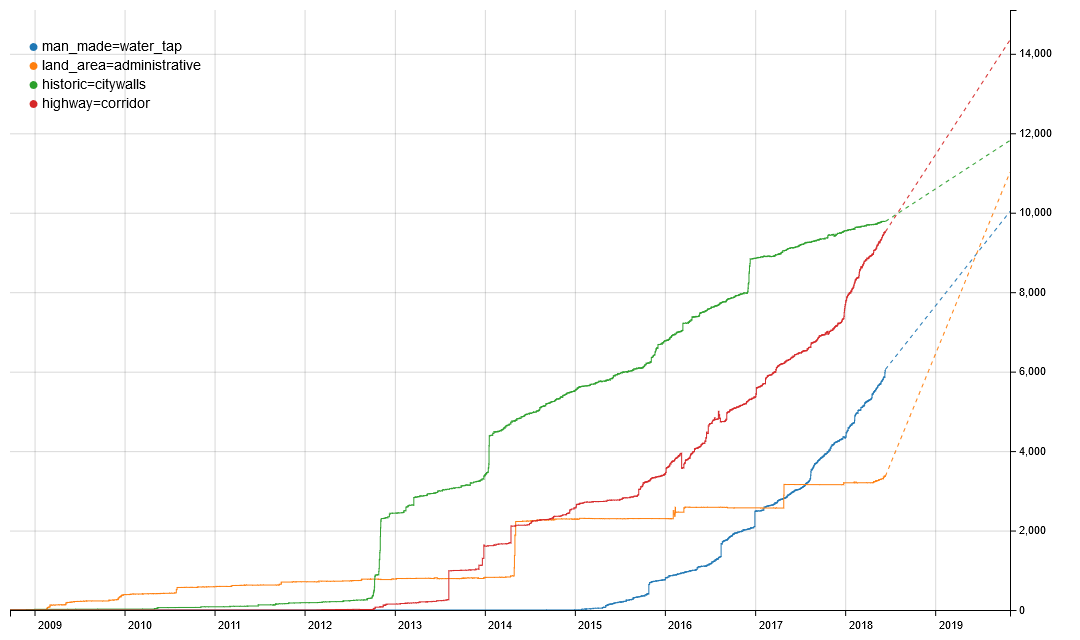
Some new tags have reached 10.000 occurrences:
osmwiki:Tag:attraction=animal ✔ added, see comment:3
osmwiki:Tag:highway=corridor
osmwiki:Tag:historic=citywalls ✔ added, see #9164
osmwiki:Tag:land_area=administrative × see comment:13
osmwiki:Tag:man_made=water_tap
taginfo:tags/attraction=animal#map
taginfo:tags/highway=corridor#map
taginfo:tags/historic=citywalls#map
taginfo:tags/land_area=administrative#map
taginfo:tags/man_made=water_tap#map
Attachments (1)
Change History (29)
comment:1 by , 8 years ago
| Description: | modified (diff) |
|---|
comment:2 by , 8 years ago
| Description: | modified (diff) |
|---|
comment:3 by , 8 years ago
comment:4 by , 7 years ago
I would add highway=corridor for now. So far I think indoor mapping and a common tagging schema has not really evolved yet in OSM. (osmwiki:Simple_Indoor_Tagging uses indoor=corridor instead)
comment:6 by , 7 years ago
Lol. I just noticed I made a big typo. What I wanted to say was "I would add highway=corridor to ignorelist for now." :D
comment:7 by , 7 years ago
Ah. I asked to Vespucci and iD developers what they are doing. I think we should add this to our presets, but I have no idea if we should prefer highway or indoor.
comment:8 by , 7 years ago
From the comments I received I think it's fine to add highway=corridor. iD already has it anyway.
comment:9 by , 7 years ago
| Keywords: | historic citywalls added |
|---|---|
| Summary: | highway=corridor, attraction=animal → highway=corridor, attraction=animal, historic=citywalls |
By the way now we must decide for historic=citywalls
comment:10 by , 7 years ago
| Description: | modified (diff) |
|---|---|
| Summary: | highway=corridor, attraction=animal, historic=citywalls → highway=corridor, attraction=animal, historic=citywalls, land_area=administrative |
comment:12 by , 7 years ago
| Milestone: | 18.09 → 18.10 |
|---|
comment:13 by , 7 years ago
| Description: | modified (diff) |
|---|
land_area=administrative is used only about 5500 times (maybe there was an reverted import that created a peak >10k?), is used only on two hot spots global and has no real wiki documentation.
osmwiki:Tag:historic=citywalls is a duplicate to osmwiki:Tag:barrier=city_wall to me.
comment:14 by , 7 years ago
| Milestone: | 18.10 → 18.11 |
|---|
comment:15 by , 7 years ago
osmwiki:Tag:historic=citywalls is a duplicate to osmwiki:Tag:barrier=city_wall to me.
Is there any case of city walls that are not historic nowadays?
comment:16 by , 7 years ago
Wait! There is case where historic=citywalls makes case.
Ruined citywalls, maybe to the point where only foundations remain are no longer barrier=*, but are still historic.
For me this tag makes sense and I would support supporting it in JOSM.
comment:17 by , 7 years ago
| Milestone: | 18.11 → 18.12 |
|---|
comment:18 by , 7 years ago
| Milestone: | 18.12 → 19.01 |
|---|
comment:19 by , 7 years ago
| Milestone: | 19.01 → 19.02 |
|---|
comment:20 by , 7 years ago
| Milestone: | 19.02 → 19.03 |
|---|
comment:21 by , 7 years ago
| Description: | modified (diff) |
|---|
comment:22 by , 7 years ago
| Description: | modified (diff) |
|---|
comment:23 by , 7 years ago
| Milestone: | 19.03 → 19.04 |
|---|
comment:24 by , 7 years ago
| Milestone: | 19.04 → 19.05 |
|---|
comment:26 by , 6 years ago
| Description: | modified (diff) |
|---|---|
| Summary: | highway=corridor, attraction=animal, historic=citywalls, land_area=administrative → highway=corridor, attraction=animal, historic=citywalls, land_area=administrative, man_made=water_tap |
by , 6 years ago
| Attachment: | taghistory.png added |
|---|
comment:28 by , 6 years ago
| Description: | modified (diff) |
|---|---|
| Summary: | highway=corridor, attraction=animal, historic=citywalls, land_area=administrative, man_made=water_tap → Add highway=corridor, attraction=animal, man_made=water_tap |



In 14181/josm: